6 4: Present Value of Annuities and Installment Payment Mathematics LibreTexts

You buy an annuity either with a single payment or a series of payments, and you receive a lump-sum payout shortly after purchasing the annuity or a series of payouts over time. Future value, on the other hand, is a measure of how much a series of regular payments will be worth at some point in the future, given a set interest rate. If you’re making regular payments what are temporary accounts fanda glossary on a mortgage, for example, calculating the future value can help you determine the total cost of the loan. To determine how much an annuity is worth, a prospective investor will need to start by calculating its present value. The present value of an annuity is the amount of money an investor will need to invest today to secure annuity payments in the future.

Why Do You Need to Know Present and Future Value?

• If you chose to enter a future lump sum, this result represents the periodic payment amount needed to pay off the loan within the specified time period.
• You probably noticed that our NPV calculator determines two values as results.
• This can be an expected return on investment or a current interest rate.
• These recurring or ongoing payments are technically referred to as annuities (not to be confused with the financial product called an annuity, though the two are related).
• The discount rate is a key factor in calculating the present value of an annuity.
• The internal rate of return (IRR calculator) of a project is such a discount rate at which the NPV equals zero.

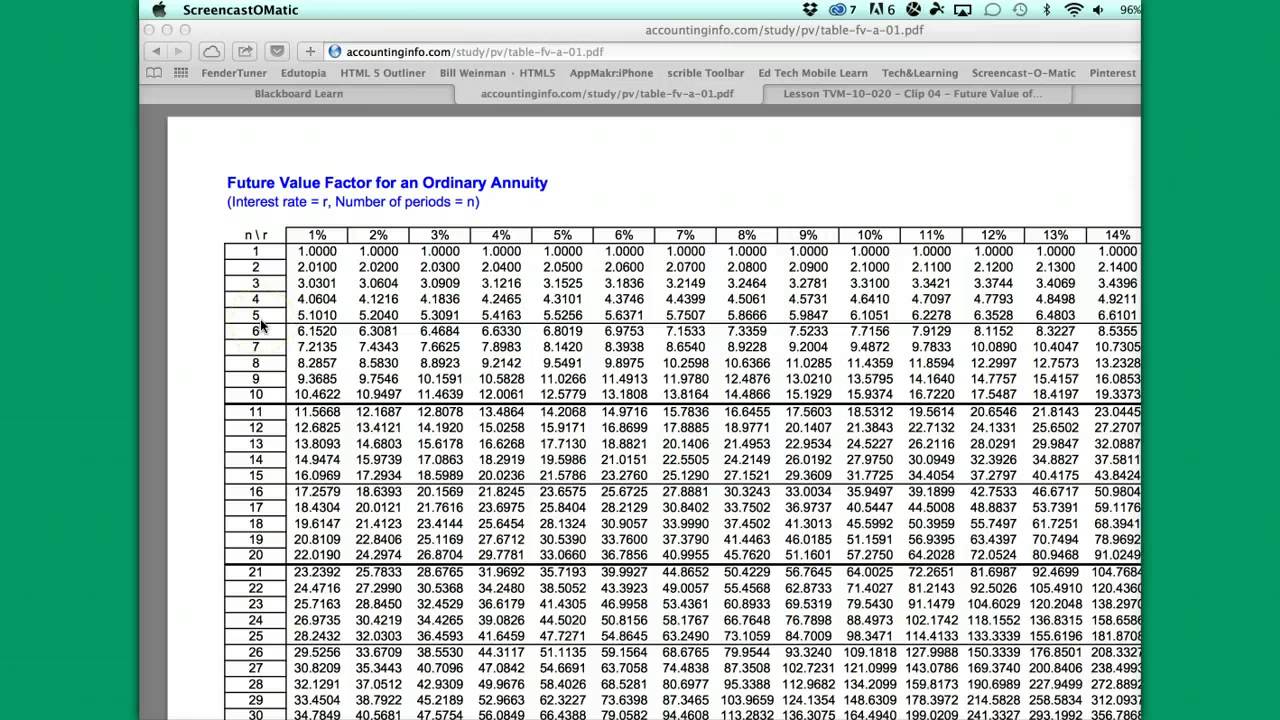
The series of payments can be either deposits (with positive signs) or withdrawal (with negative signs). Therefore, if you make regular deposits into a savings account, monthly home mortgage, monthly insurance account or pension plan, you happen to face an annuity. An ordinary annuity is a series of equal payments made at the end of consecutive periods over a fixed length of time. The payment for an annuity due is made at the beginning of each period. This variance in when the payments are made results in different present and future value calculations. Based on your entries, this is the present value of the annuity you entered information for.

Everything You Need To Master Financial Modeling

On this page, you can calculate present value of annuity (PVA) of both simple as well as complex annuities. You can use this calculator to calculate loan repayments and payouts from immediate insurance schemes. The present value of an annuity refers to how much money would be needed today to fund a series of future annuity payments. Or, put another way, it’s the sum that must be invested now to guarantee a desired payment in the future. Present value tells you how much money you would need now to produce a series of payments in the future, assuming a set interest rate.

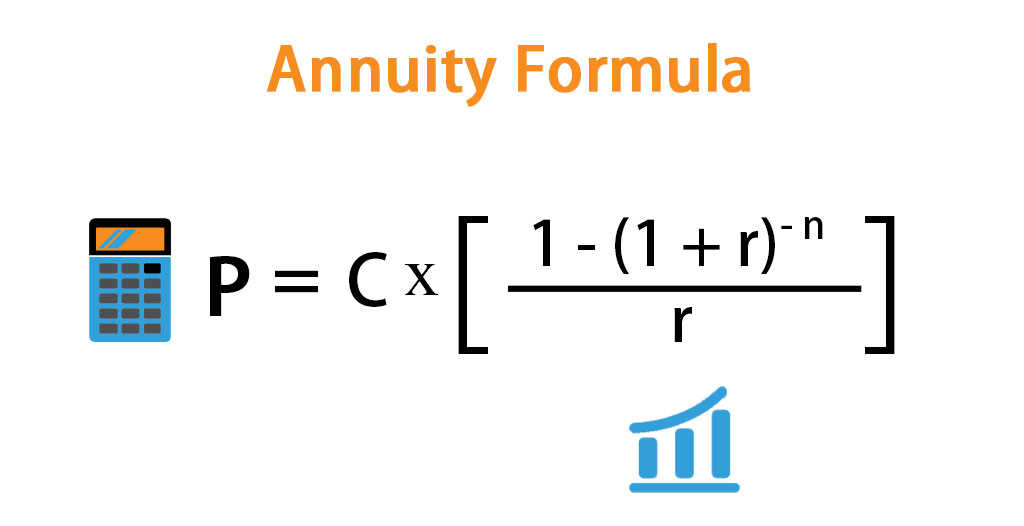
Everyday Calculation

To account for payments occurring at the beginning of each period, the ordinary annuity FV formula above requires a slight modification. In contrast to the FV calculation, PV calculation tells you how much money would be required now to produce a series of payments in the future, again assuming a set interest rate. If you are considering investing in annuities, you will want to explore the different options available and use the annuity calculators to try out different investment scenarios. An annuity is a financial product that provides a stream of payments to an individual over a period of time, typically in the form of regular installments. Annuities can be either immediate or deferred, depending on when the payments begin. Immediate annuities start paying out right away, while deferred annuities have a delay before payments begin.

Present Value of Annuity Calculation Example (PV)

The first one is NPV, and the second is called the “expected cash flow”. Wolfram|Alpha can quickly and easily compute the present value of money, as well as the amount you would need to invest in order to achieve a desired financial goal in the future. Plots are automatically generated to help you visualize the effect that different interest rates, interest periods or future values could have on your result. The future value of an annuity refers to how much money you’ll get in the future based on the rate of return, or discount rate.

How to calculate net present value?

The present value of an annuity can be used to determine whether it is more beneficial to receive a lump-sum payment or an annuity spread out over a number of years. The present value of annuity calculator is a handy tool that helps you to find the value of a series of equal future cash flows over a given time. In other words, with this annuity calculator, you can compute the present value of a series of periodic payments to be received at some point in the future. For example, a court settlement might entitle the recipient to $2,000 per month for 30 years, but the receiving party may be uncomfortable getting paid over time and request a cash settlement. The equivalent value would then be determined by using the present value of annuity formula. The result will be a present value cash settlement that will be less than the sum total of all the future payments because of discounting (time value of money).

One of the most common problems deals with finding the balance owed at a given time during the life of a loan. Suppose a person buys a house and amortizes the loan over 30 years, but decides to sell the house a few years later. At the time of the sale, he is obligated to pay off his lender, therefore, he needs to know the balance he owes. Since most long term loans are paid off prematurely, we are often confronted with this problem. Therefore, the monthly payment needed to repay the loan is $934.13 for five years.

Present value of an annuity is a time value of money formula used for measuring the current value of a future series of equal cash flows. This calculator will calculate the present value of an annuity starting with either a future lump sum, or with a future payment amount. What that means is the discounted present value of a $10,000 lump sum payment in 5 years is roughly equal to $7,129.86 today at a discount rate of 7%. For example, you could use this formula to calculate the PV of your future rent payments as specified in your lease.